Понятие электрической цепи и ее составные части

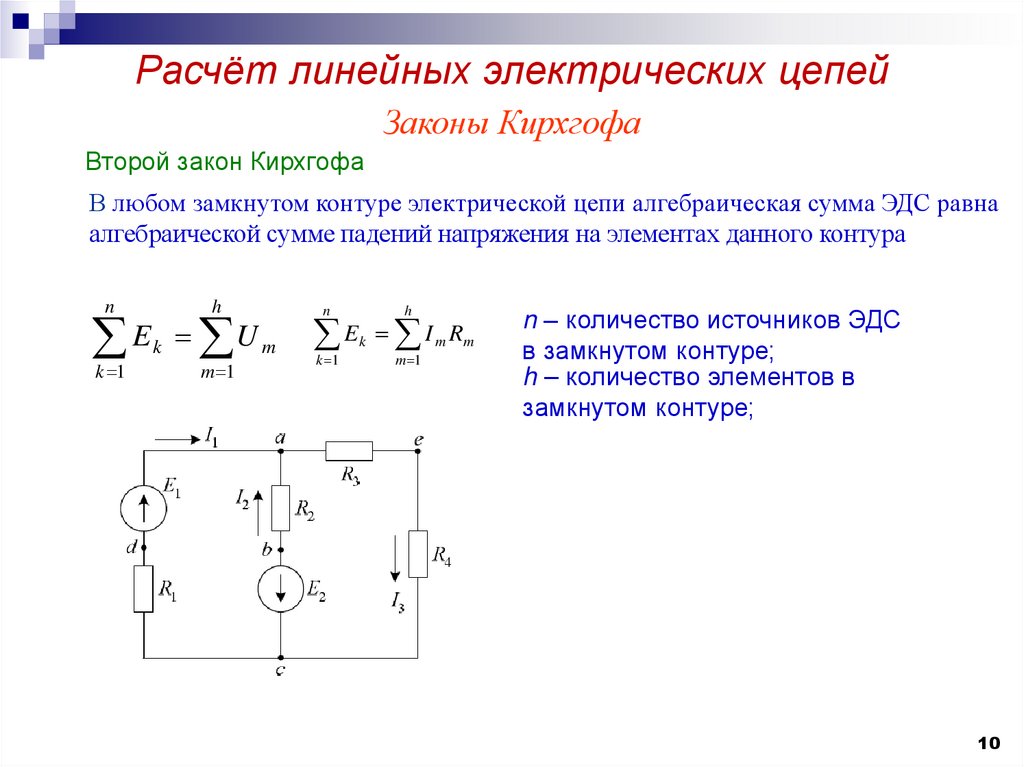
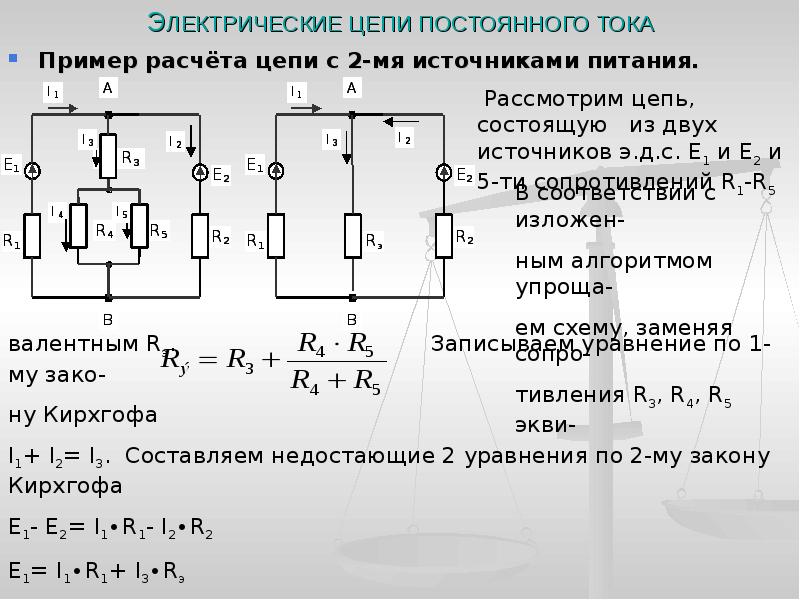
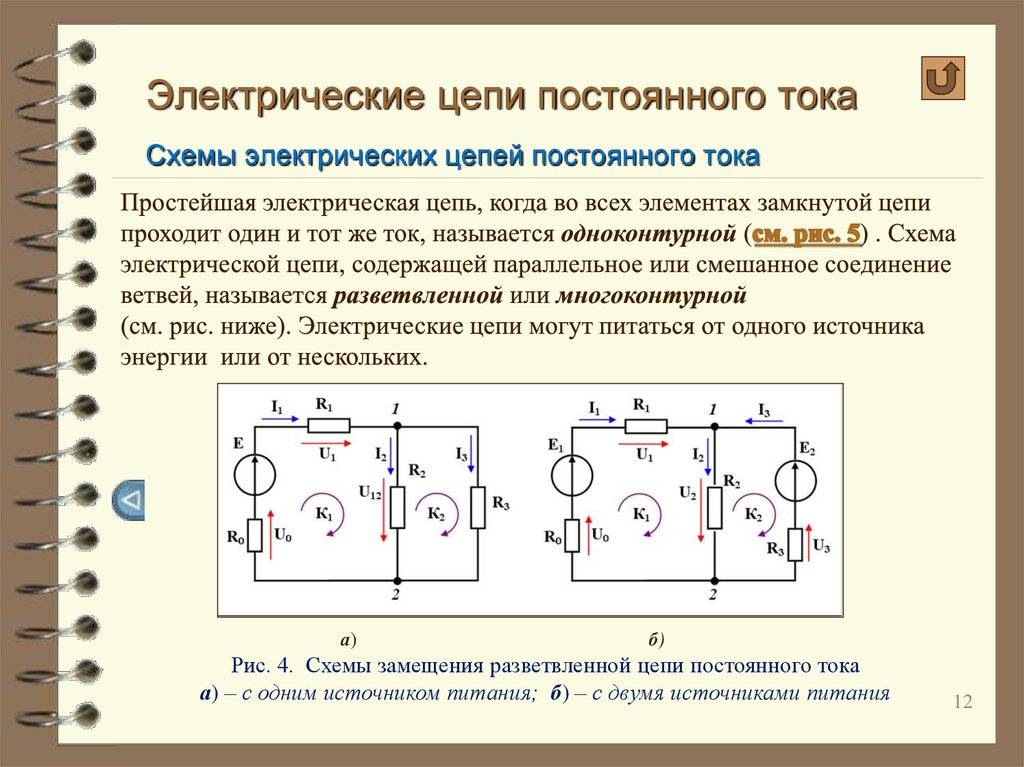
Выключатель ножевого типа

Возможно, лучший вид переключателя для иллюстрации принципа действия — это выключатель ножевого типа:

Рисунок 4 – Выключатель ножевого типа

Ножевой переключатель – это не что иное, как токопроводящий рычаг, свободно поворачивающийся на шарнире, вступающий в физический контакт с одним или несколькими неподвижными контактами, которые также являются токопроводящими. Переключатель, показанный на приведенном выше рисунке, собран на фарфоровом основании (отличный изоляционный материал), с использованием меди (отличный проводник) для «лезвия» и контактов. Ручка сделана из пластика, чтобы изолировать руку оператора от токопроводящего лезвия переключателя при его открытии или закрытии. Ниже показан еще один тип переключателя, с двумя неподвижными контактами вместо одного:

Рисунок 5 – Переключатель ножевого типа с 3-мя контактами

Ножевой переключатель, показанный здесь, имеет одно «лезвие» и два неподвижных контакта, что означает, что он может включать или выключать более одной цепи

На данный момент это не так важно, чтобы просто понять основную идею того, что такое ключ, и как он работает. Ножевые переключатели отлично подходят для иллюстрации основного принципа работы ключа, но они представляют определенные проблемы безопасности при использовании в электрических цепях большой мощности. Открытые проводники переключателя делают очень возможным случайный контакт с цепью, а любая искра, которая может возникнуть между движущимся ножом и неподвижным контактом, может воспламенить любые находящиеся поблизости горючие материалы

В большинстве современных конструкций переключателей движущиеся проводники и контакты закрыты изолирующим кожухом, чтобы уменьшить эти опасности. Фотографии нескольких современных типов переключателей показывают, что механизмы переключения гораздо более скрыты, чем в конструкции ножевого выключателя:

Открытые проводники переключателя делают очень возможным случайный контакт с цепью, а любая искра, которая может возникнуть между движущимся ножом и неподвижным контактом, может воспламенить любые находящиеся поблизости горючие материалы. В большинстве современных конструкций переключателей движущиеся проводники и контакты закрыты изолирующим кожухом, чтобы уменьшить эти опасности. Фотографии нескольких современных типов переключателей показывают, что механизмы переключения гораздо более скрыты, чем в конструкции ножевого выключателя:

Рисунок 6 – Сравнение размеров переключателей

Условные обозначения источников электрической энергии и элементов цепей

Условное обозначение	Элемент
	Идеальный источник ЭДС Е – электродвижущая сила, Е = const Ro = 0 – внутреннее сопротивление
	Идеальный источник тока I = const Rвн- внутреннее сопротивление источника тока, Rвн>>Rнаг
	Активное сопротивление R = const
	Индуктивность L = const
	Емкость С = const

К химическим источникам тока относят гальванические элементы и аккумуляторы. В них заряды переносятся в результате химических реакций. При этом в гальваническом элементе реагенты расходуются необратимо, а в аккумуляторе они могут восстанавливаться путем пропускания через аккумулятор электрического тока противоположного направления от других источников.

Источники электрической энергии относятся к группе активных элементов электротехнических устройств. Если Rо=0 и электродвижущая сила (ЭДС) Е=const, то источник называется идеальным. Аккумуляторная батарея по своим параметрам близка к идеальному источнику ЭДС.

К группе пассивных элементов относятся: активное сопротивление R, индуктивность L и емкость С.

В электротехнических устройствах одновременно протекают три энергетических процесса:

1 В активном сопротивлении в соответствии с законом Джоуля – Ленца происходит преобразование электрической энергии в тепло.

Мощность, по определению равна отношению работы к промежутку времени, за который эта работа совершается. Следовательно, мощность тока для участка цепи

p = A/t = ui

Полная мощность, вырабатываемая генератором, равна

где R- полное сопротивление замкнутой цепи, называемое омическим или активным;

Р, I – мощность и ток в цепи постоянного тока.

р, i, и – мгновенные значения активной мощности, тока и напряжения в цепи переменного тока,

g – активная проводимость или величина, обратная сопротивлению g=1/R измеряется в сименсах (См).

В соответствии с законом сохранения энергии работа есть мера изменения различных видов энергии. Так, в электродвигателе за счет работы тока возникает механическая энергия, протекают химические реакции и т. д. На резисторах происходит необратимое преобразование энергии электрического тока во внутреннюю энергию проводника.

Если в проводнике под действием тока не происходит химических реакций, то температура проводника должна измениться. Изменение внутренней энергии проводника (количество теплоты) Q равно работе А, которую совершает суммарное поле при перемещении зарядов:

Q = А = uit

Воспользовавшись законом Ома, получим два эквивалентных выражения:

Это и есть закон Джоуля – Ленца.

Если нужно сравнить два резистора по характеру тепловых процессов, происходящих в них, то нужно предварительно выяснить: протекает ли по ним одинаковый ток или они находятся под одинаковым напряжением?

Если по двум резисторам протекают одинаковые токи, то согласно формуле за одно и то же время больше возрастает внутренняя энергия резистора с большим сопротивлением. С таким случаем мы встречаемся, например, в цепи с последовательным соединением резисторов. Последнее обстоятельство следует учитывать при включении в сеть нагрузки (электроплиток, утюгов, электродвигателей и т. д.). Сопротивление подводящих проводов при этом должно быть значительно меньше, чем сопротивление нагрузки. При несоблюдении этого условия в проводах выделится большое количество теплоты, что может привести к их загоранию.

Если же оба резистора находятся под одинаковым напряжением, то согласно формуле быстрее будет нагреваться резистор с меньшим сопротивлением. Такой эффект, в частности, наблюдают при параллельном соединении резисторов.

Термин “сопротивление” применяется для условного обозначения элемента электрической цепи и для количественной оценки величины R.

Сопротивление измеряется в омах (Ом). 1 Ом – это сопротивление проводника, сила тока в котором равна 1 А, если на концах его поддерживается разность потенциалов 1 В:

1 Ом = 1 В/1 А

Электрическое сопротивление R материалов с изменением температуры меняется. Сопротивление металлических проводников линейно возрастает с температурой. У полупроводников и электролитов с увеличением температуры удельное сопротивление уменьшается, причем нелинейно.

Для сравнения проводников по степени зависимости их сопротивления от температуры t вводится величина a, называемая температурным коэффициентом сопротивления. Отсюда

Для практических расчетов в электрических цепях величину R можно принимать постоянной. В этом случае зависимость напряжения на сопротивлении R от силы тока (вольт-амперная характеристика) будет называться линейной. Электрические цепи, в которые включены постоянные по величине сопротивления, также будут линейными.

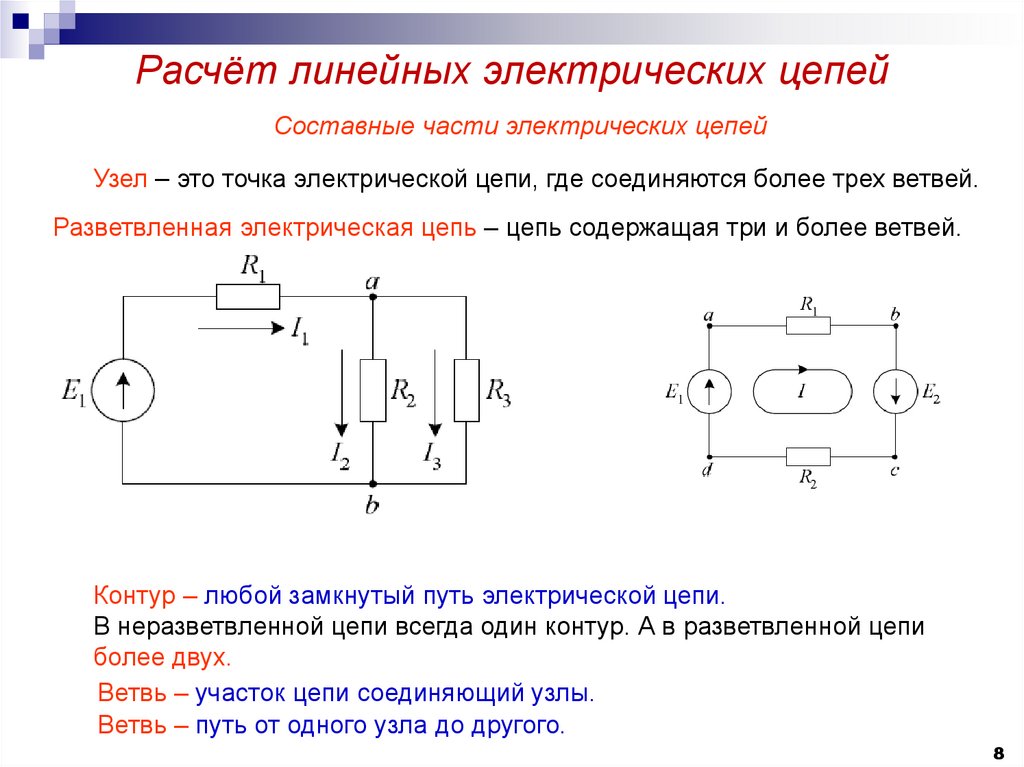
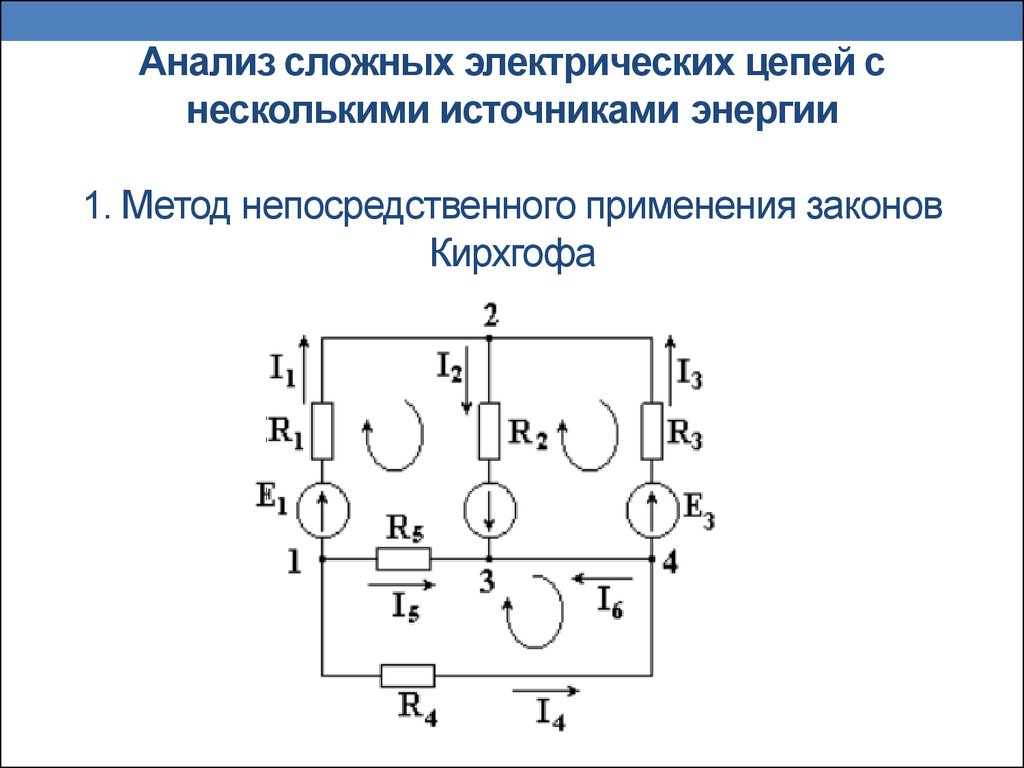
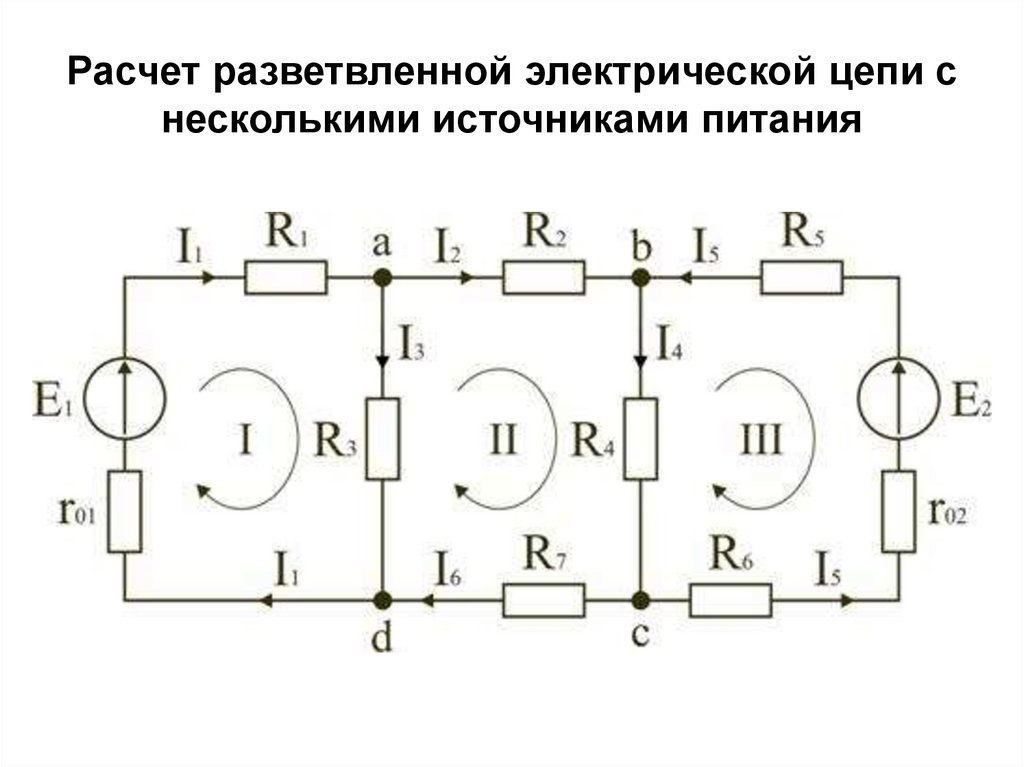
Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

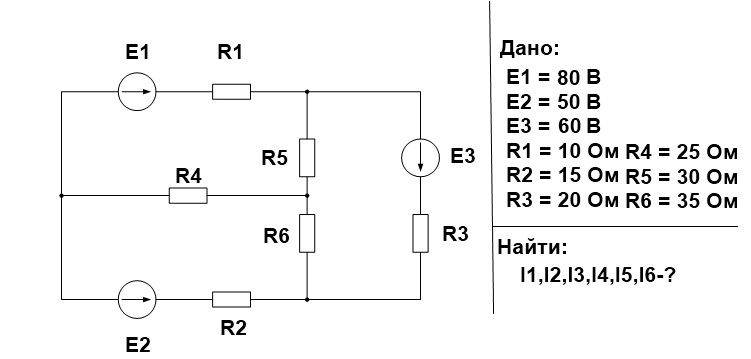
Выполняем все поэтапно.

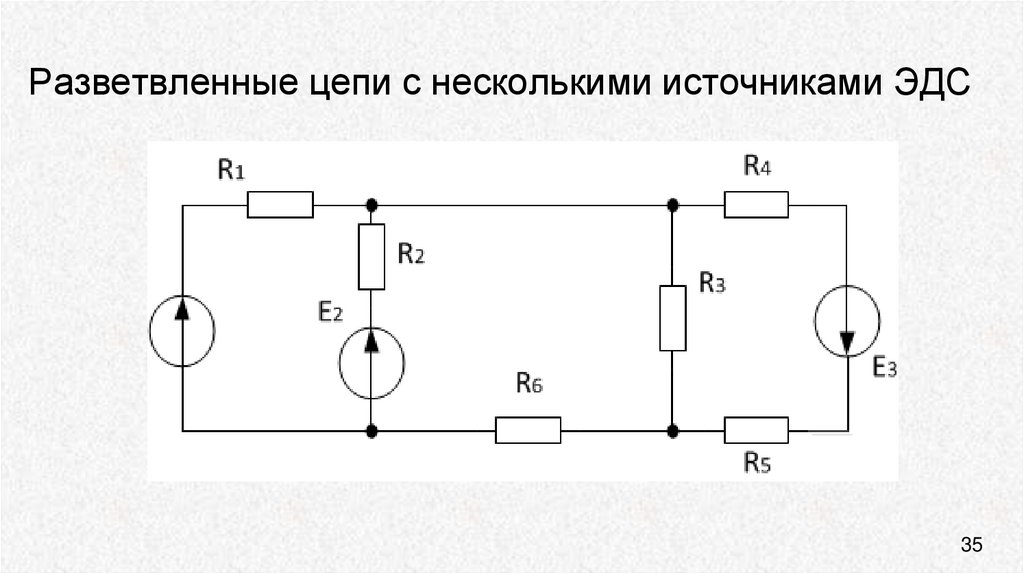
1. Произвольно выбираем направления действительных токов I₁-I₆.

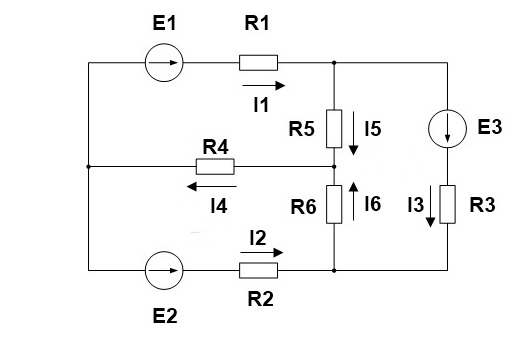
2.Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.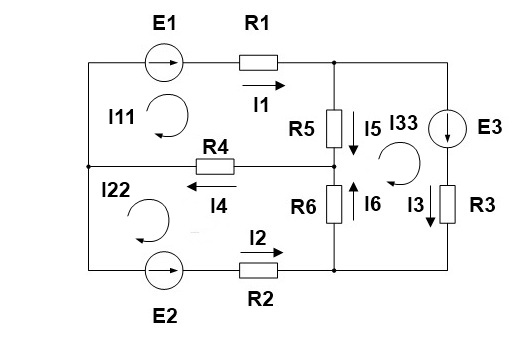

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом: 

Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура.  Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему: 

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.  

5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус. 

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

А для остальных

Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!

Рекомендуем – Метод двух узлов

Просмотров: 204542

Электрическая цепь и ее элементы

Режимы работы элементов и электрических цепей

Электрическая цепь — это совокупность устройств и объектов, образующих путь электрического тока. Отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определенную функцию, называется элементом электрической цепи.

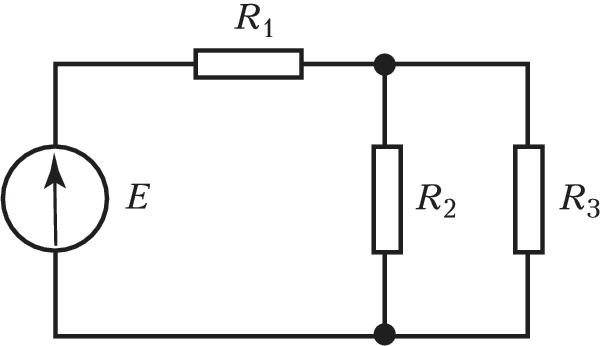
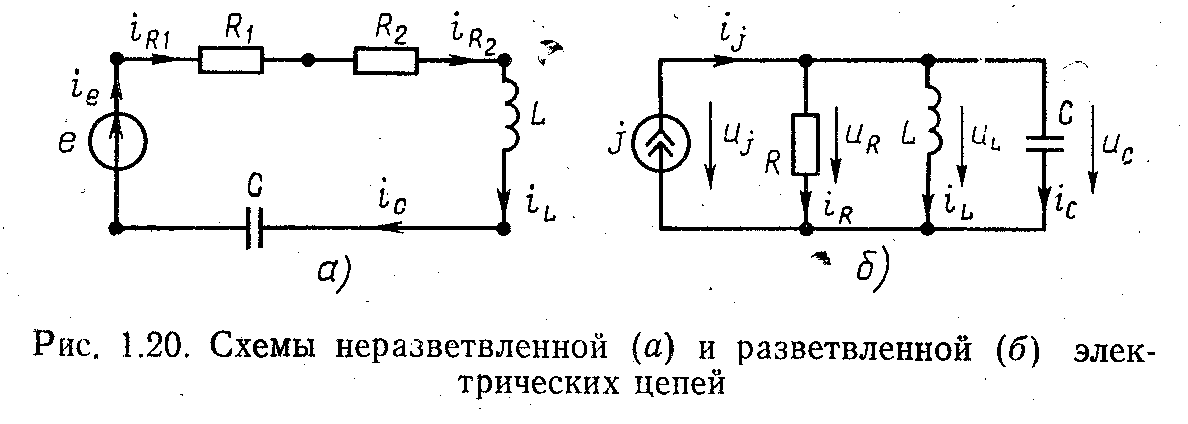
Простейшей электрическая цепь состоит из следующих элементов: 1 — источник электрической энергии; 2 — приемники электрической энергии; 3 — соединительные провода (рис. 1.10).

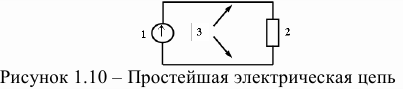
Источник электрической энергии дает электрическую энергию, потребитель эту энергию преобразует в другие виды энергии: свет, тепло, движение и т. д

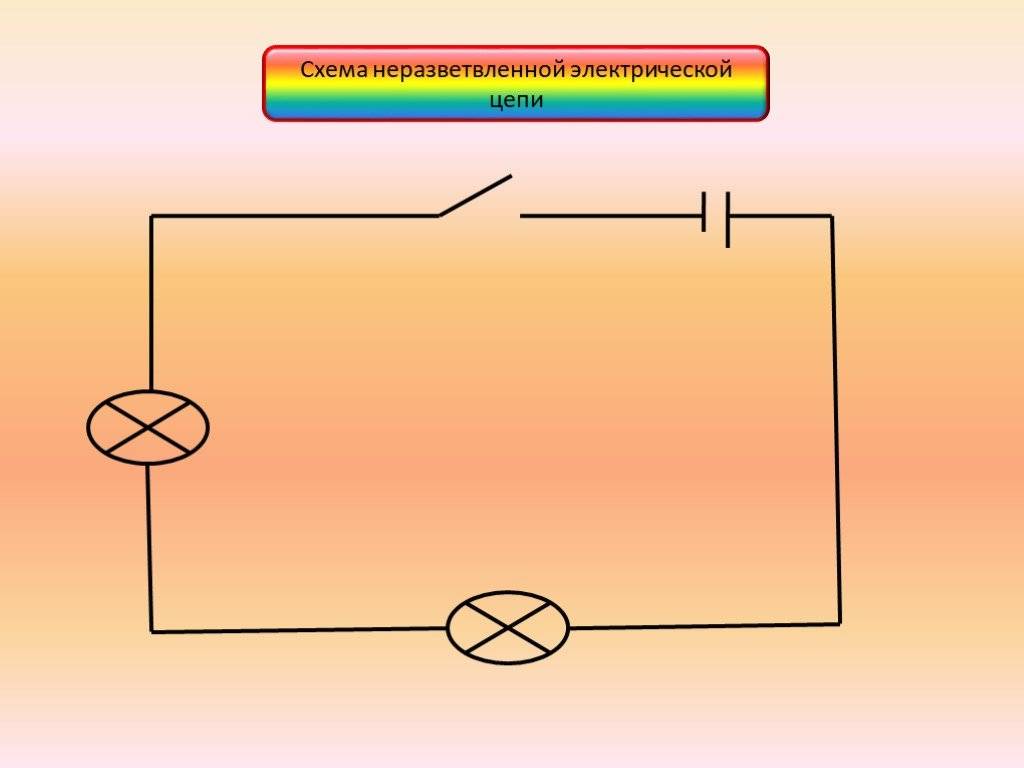
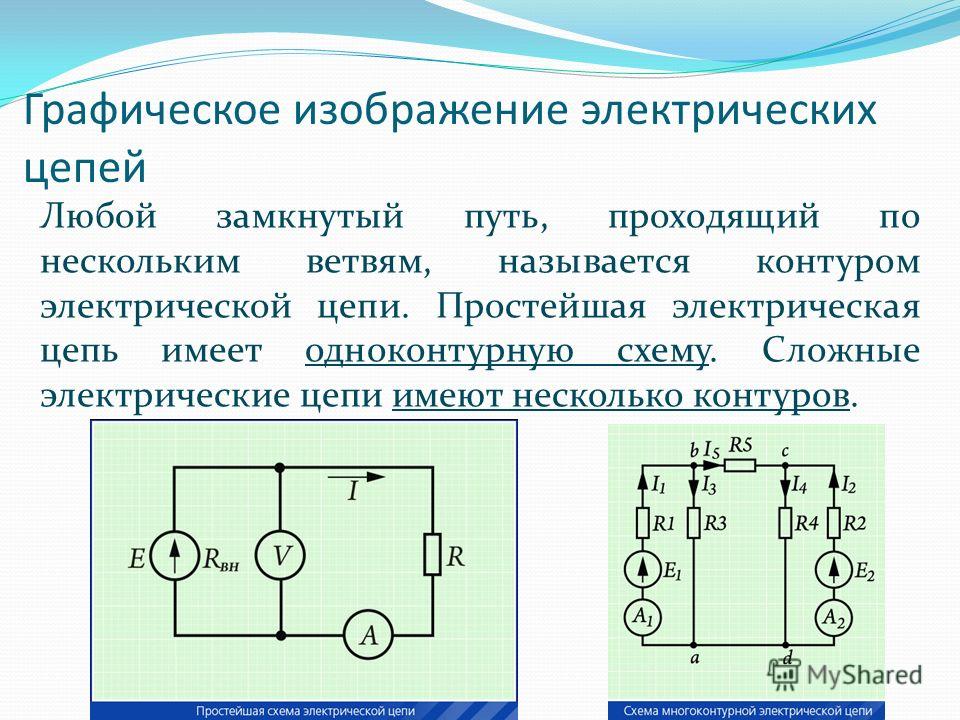
Схема электрической цепи — это графическое изображение электрической цепи, содержащее условные обозначения ее элементов, показывающее соединения этих элементов.

Типы схем: структурная; функциональная; принципиальная; монтажная и др.

На принципиальной схеме приводится полный состав элементов и указаны все связи между ними.

Функциональные электрические схемы — это наиболее общие схемы в отношении уровня абстракции и обычно показывают лишь функциональные связи между составляющими данного объекта и раскрывающими его сущность и дающие представление о функциях объекта, изображённого на данном чертеже.

Принципиальные электрические схемы — это чертежи, показывающие полные электрические и магнитные и электромагнитные связи элементов объекта, а также параметры компонентов, составляющих объект, изображённый на чертеже.

Монтажные схемы — это чертежи, показывающие реальное расположение компонентов как внутри, так и снаружи объекта, изображённого на схеме.

Наиболее характерными для электрических цепей являются следующие режимы работы: номинальный, рабочий, холостого хода и короткого замыкания.

Номинальным называется режим, при котором данный элемент электрической цепи работает со значениями различных величин (тока, напряжения и др.), на которые он рассчитан заводом-изготовителем, а которые называются его номинальными (или техническими) данными. Номинальные данные указываются в справочной литературе, технической документации или на самом элементе.

Рабочим называется режим, при котором мощность, отдаваемая источником или потребляемая приемником, достигает максимального значения.

Под режимом холостого хода понимается такой режим, при котором приемник отключен от источника. При этом источник не отдает энергию во внешнюю цепь, а приемник не потребляет ее.

Режимом короткого замыкания называется режим, возникающий при соединении между собой выводов источника, приемника или соединительных проводов, а также иных элементов электрической цепи, между которыми имеется напряжение. При этом сопротивление в месте соединения оказывается практически равным нулю. Режим короткого замыкания в электрических установках нежелателен так как он приводит к большому току (больше номинального), т. е. к резкому увеличению выделения тепла и выходу из строя аппаратуры.

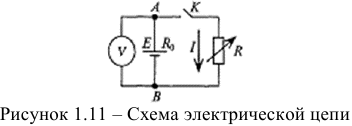
Параметры, характеризующие работу электрической цепи (рис. 1.11) при различных режимах, определяются следующими выражениями.

Ток в замкнутой цепи

Напряжение на клеммах источника

Падение напряжения на сопротивлении источника

Полезная мощность (мощность потребителя)

Исследуем изменение этих величин при изменении сопротивления от бесконечности (режим холостого хода) до нуля (режим короткого замыкания).

В режиме холостого хода (ключ разомкнут)

В режиме короткого замыкания

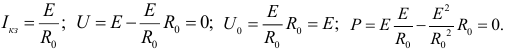
Максимальная полезная мощность выделяется при .

При максимальной отдаче мощности ток в цепи равен

а коэффициент полезного действия

так как

К КПД цепи приближается в режиме, близкой к холостому ходу. Зависимости напряжения и полезной мощности от нагрузки (тока ) показаны на рисунке 1.12.

Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):

Возможно эти страницы вам будут полезны:

ЭДС и напряжение в электрической цепи. Электродвижущая сила. Энергия и мощность электрического тока. Баланс мощностей

Закон Ома. Электрическое сопротивление. Закон Джоуля-Ленца

Режимы работы источников тока. Потенциальная диаграмма

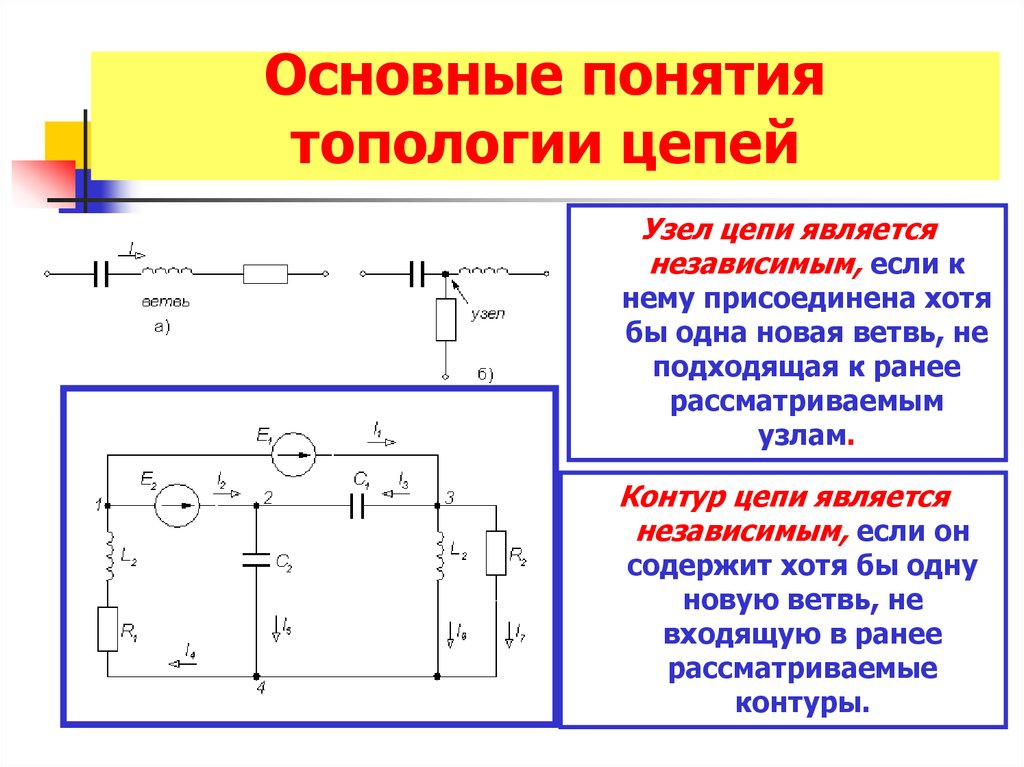
Ветвь, узел, контур электрической цепи. Законы Кирхгофа

Схемы электрических цепей

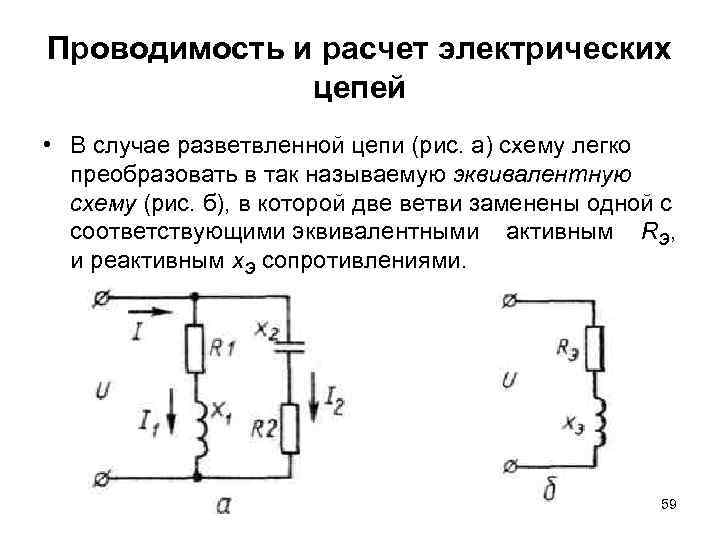
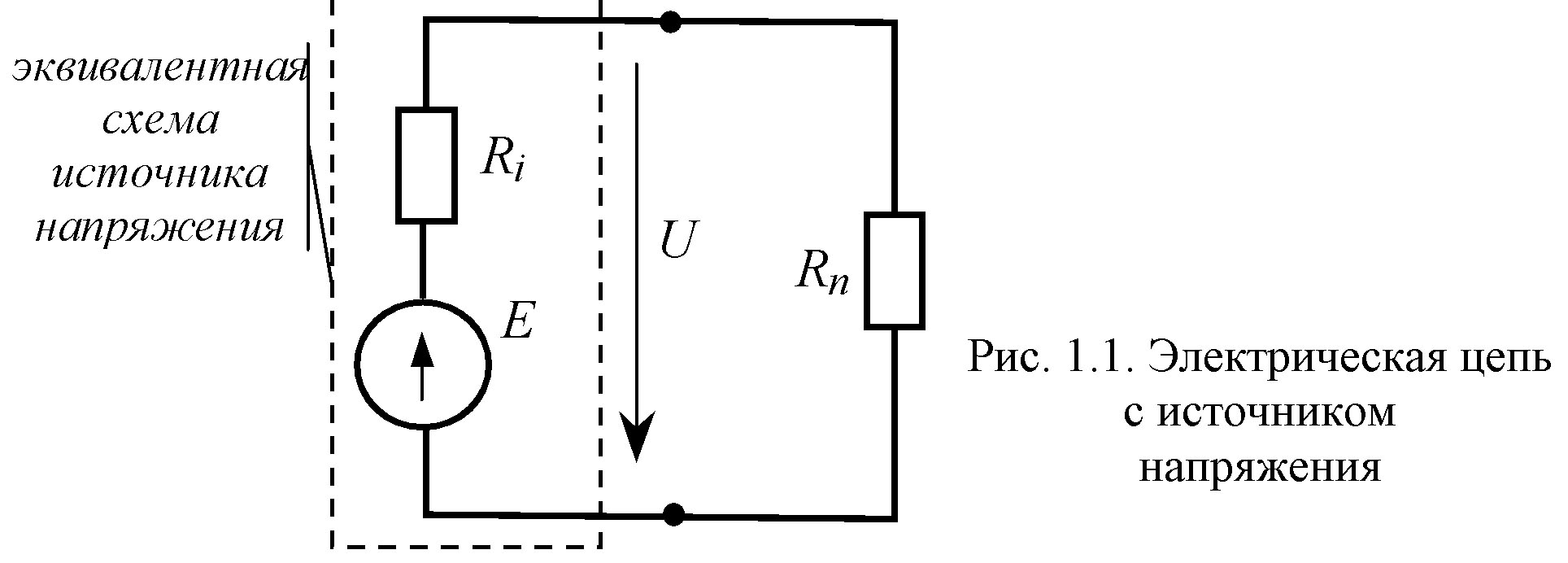
Схемы электрических цепей являются графическим представлением электрической цепи и позволяют наглядно представить расположение и взаимосвязь ее элементов. Схемы электрических цепей используются для проектирования, анализа и понимания работы различных электрических систем и устройств.

Схема электрической цепи состоит из символов, отображающих отдельные элементы цепи, и линий, обозначающих проводники, по которым проходит электрический ток. В схеме указывается направление тока, с помощью стрелки, и подписывается напряжение на каждом элементе.

Наиболее распространенными элементами, встречающимися в схемах электрических цепей, являются резисторы, конденсаторы, индуктивности, источники тока и напряжения, ключи и транзисторы. В схемах также могут быть представлены и другие элементы, специфичные для конкретного устройства или системы.

• Резисторы представляют собой элементы, ограничивающие протекание тока в цепи. Они обозначаются прямоугольником с указанием значения сопротивления.
• Конденсаторы служат для накопления и хранения электрического заряда. Они представляются двумя параллельными пластинами с указанием емкости.
• Индуктивности используются для хранения энергии в магнитном поле. Они обозначаются спиралью с указанием значения индуктивности.
• Источники тока и напряжения представляются стрелками, указывающими направление тока или напряжение. Они могут быть как постоянными, так и переменными.
• Ключи и транзисторы используются для управления протеканием тока или изменения напряжения в цепи. Они обозначаются специальными символами и подписями.

Схемы электрических цепей очень полезны при разработке новых электрических систем и устройств, а также при ремонте и техническом обслуживании существующих. Они облегчают понимание взаимосвязей между элементами цепи и позволяют предсказать и анализировать их поведение в различных условиях.

Кроме того, схемы электрических цепей часто используются для обучения студентов и стажировки специалистов в области электротехники и электроники. Они помогают разобраться в базовых принципах работы электрических систем и устройств и развивают навыки анализа и проектирования.

Последовательное соединение элементов

Последовательное соединение элементов — это один из основных типов соединений элементов в электрической цепи. В таком типе соединения элементы располагаются последовательно друг за другом, таким образом, электрический ток проходит через каждый элемент по очереди.

В последовательной цепи суммарное сопротивление равно сумме сопротивлений каждого элемента, а суммарный ток во всех элементах одинаковый. Данная характеристика позволяет определить общее сопротивление цепи по формуле: общее сопротивление равно сумме сопротивлений каждого элемента.

Последовательное соединение элементов также влияет на напряжение в цепи. Напряжение разделяется между элементами пропорционально их сопротивлениям. Таким образом, в последовательной цепи напряжение в каждом элементе может быть разным.

Последовательное соединение элементов часто используется в различных электрических устройствах. Оно позволяет объединить несколько элементов в одну цепь и эффективно распределить электрический ток и напряжение между ними.

Например, в последовательно соединенной цепи сопротивления, если одно из сопротивлений отключить или поломать, то все элементы цепи перестанут работать

Поэтому важно правильно подбирать элементы цепи и следить за их состоянием

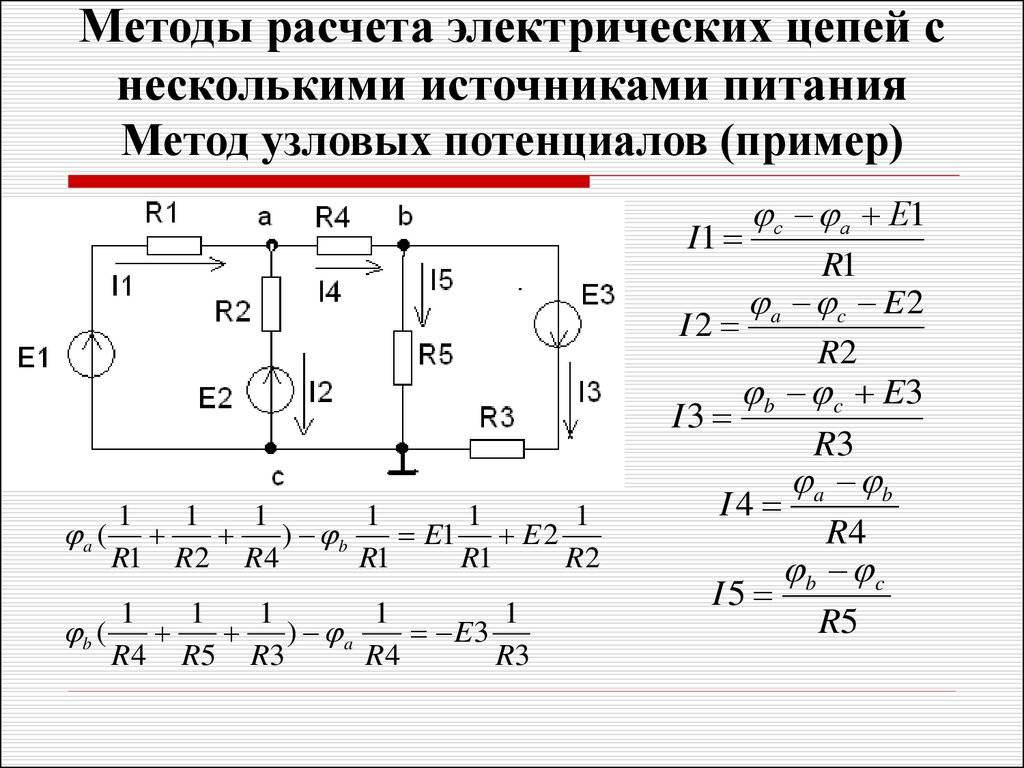
Метод узловых (потенциалов) напряжений

ТОЭ › Методы расчета цепей постоянного тока

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.

Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие. В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.

Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов)

Метод узловых потенциалов примеры решения задач

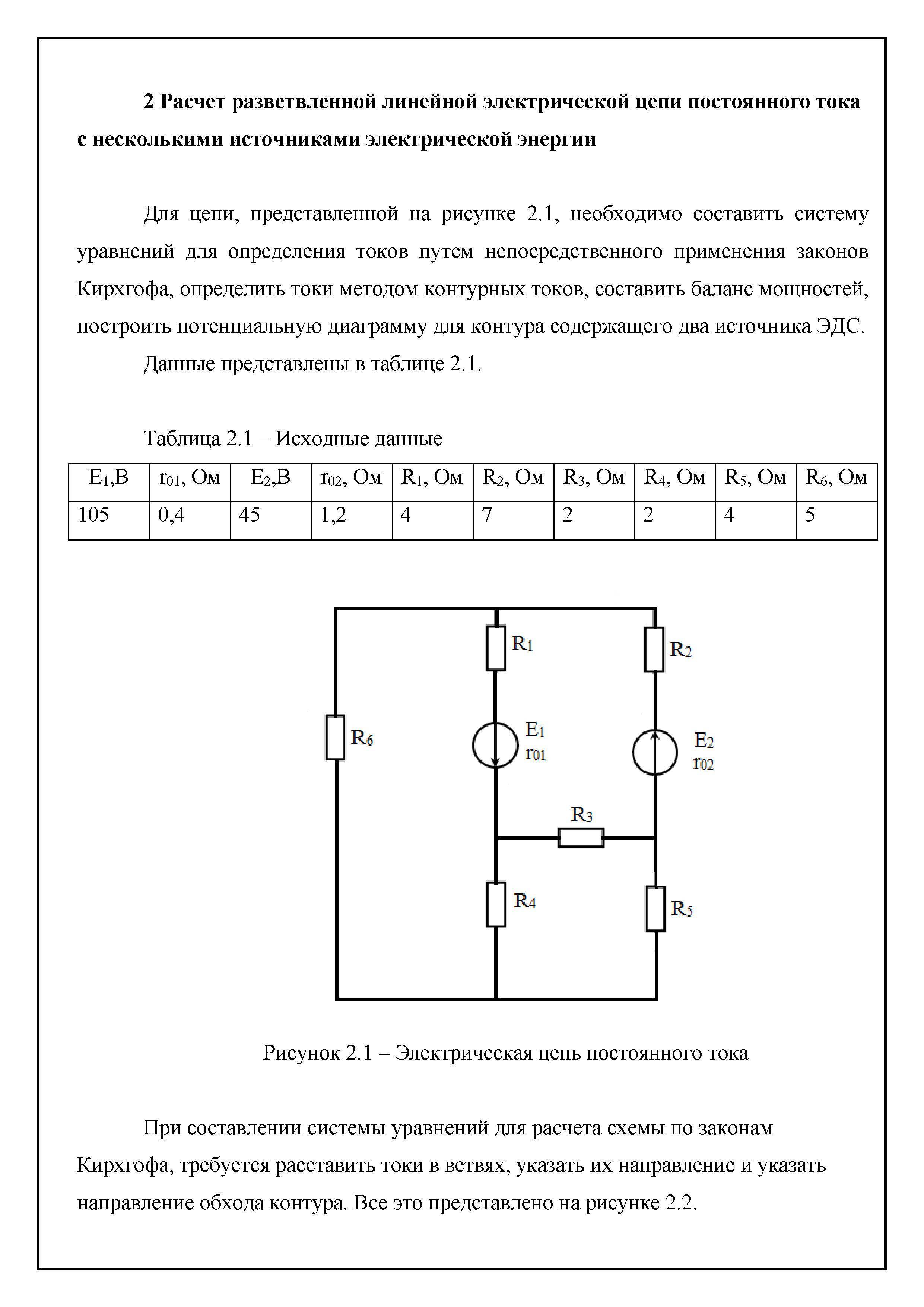
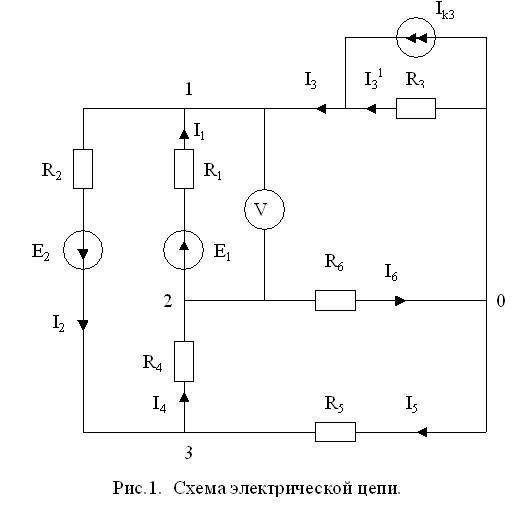
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

Рис.1. Схема постоянного тока

Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.

Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.

Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.

В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения

имеют следующий смысл:

– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

Аналогично

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

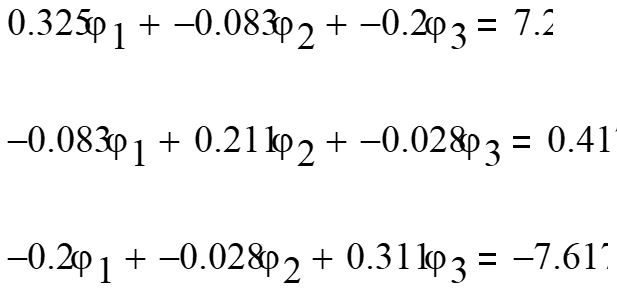
В результате получены следующие значения потенциалов в узлах цепи:

Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.

В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что

Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.

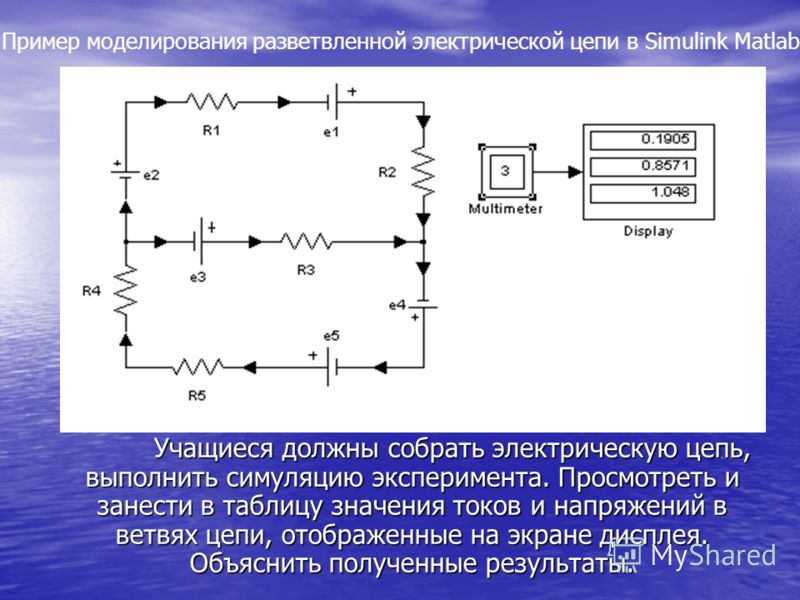
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

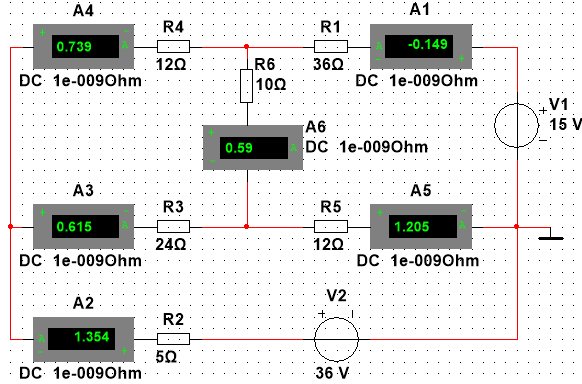Рис.2. Моделирование в Multisim

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.

Виды электрических цепей

Существует несколько видов электрических цепей, которые можно классифицировать по различным параметрам. Вот некоторые из основных видов электрических цепей:

1. По типу подключения компонентов:

   • серийная цепь: компоненты соединяются один за другим, так что ток протекает через них последовательно. Сумма напряжений на каждом компоненте равна общему напряжению источника питания;
   • параллельная цепь: компоненты соединяются параллельно, так что напряжение одинаково на каждом компоненте, а сумма токов, текущих через каждый компонент, равна общему току в цепи.

2. По характеру тока:

   • постоянный ток (DC): направление тока не меняется со временем. Ток имеет постоянное направление и величину;
   • переменный ток (AC): направление и величина тока меняются со временем. Ток периодически изменяет свое направление и значение.

3. По применению:

   • силовые цепи: используемые для передачи электрической энергии от источника питания к различным устройствам и нагрузкам, таким как освещение, электродвигатели, бытовые приборы и т.д.;
   • сигнальные цепи: для передачи сигналов и информации, например, в телекоммуникациях, радио, телевидении и других коммуникационных системах;
   • управляющие цепи: для управления и контроля различными процессами и системами, например, в системах автоматического управления, робототехнике и промышленных системах.

4. По сложности:

   • простые цепи: это цепи, состоящие из небольшого числа компонентов, таких как источник питания, резисторы и свитчи;
   • сложные цепи: состоящие из большого числа компонентов, включая интегральные схемы, транзисторы, конденсаторы, индуктивности и другие электронные компоненты.

5. Линейные и нелинейные цепи: Линейные цепи имеют компоненты, которые подчиняются линейным математическим отношениям, таким как резисторы и индуктивности. Нелинейные цепи включают компоненты, у которых нет линейной зависимости между входным и выходным сигналами, такие как диоды и транзисторы.

6. Цифровые и аналоговые цепи: Цифровые обрабатывают дискретные сигналы, представленные в виде двоичных чисел (нули и единицы), и используются в цифровой электронике, компьютерах и логических схемах. Аналоговые работают с непрерывными сигналами, представленными переменным напряжением или током, и используются в аналоговой электронике, аудио- и видеоаппаратуре.

7. Балансные и небалансные цепи: Балансные используются в системах передачи сигнала, где используется симметричное соединение, например, в симметричной аудиосистеме XLR. Небалансные — в системах, где используется одиночное соединение, например, в несимметричной аудиосистеме с разъемом RCA.

8. Открытые и закрытые цепи: В открытой нет замкнутого пути для тока. Закрытая образуется, когда проводники образуют замкнутый контур, позволяющий току протекать по цепи.